Mój post o standardzie IEEE 754 został przyjęty przez Was - czytelników - bardzo ciepło. Zaliczyliśmy nawet mały rekord odwiedzin tego dnia. Postanowiłem, że poprowadzę temat dalej. Tym razem przedstawię kilka praktycznych sposobów na to, jak można liczyć pieniądze, aby ich nie zgubić. Wszystko oczywiście - w C++! :) Zapraszam serdecznie!

Jak nie gubić pieniędzy podczas liczenia?

Okazuje się, że problem związany z liczeniem pieniędzy można rozwiązać na kilka różnych sposobów. Pomyszkowałem tu i tam i znalazłem kilka ciekawych rozwiązań i pomysłów. Każde z nich jest na swój sposób dobre, ale pamiętajmy - wszystko zależy od aktualnej potrzeby oraz ilości czasu, którym dysponujemy.

1. Wykorzystanie liczb całkowitych z wyimaginowanym przecinkiem.
2. Wykorzystanie liczb stałoprzecinkowych.
3. Modyfikacja standardu IEEE 754 - zwiększenie podstawy wykładnika.

Wykorzystanie liczb całkowitych

Pierwszym, najprostszym rozwiązaniem (które zostało przeze mnie opisane w poprzednim wpisie) jest wykorzystanie liczb całkowitych. Poprzednio jako pomysł poddałem, aby zamiast operowania na złotówkach, przejść na grosze. W praktyce, przecinek będzie nam jedynie potrzebny w momencie wyświetlenia kwoty na ekranie. Idąc dalej, nic nie stoi na przeszkodzie, abyśmy zamiast operowania na całych groszach, operowali na… tysięcznej części grosza! :) Skoro tej przecinek jest wyimaginowany, to możemy postawić go tam, gdzie tego potrzebujemy.

Jedyny problem, z którym możemy się spotkać to ograniczona pojemność typu całkowitego. Na szczęście istnieją implementacje typu BigInt, które serwują możliwość zapisu bardzo wielkich liczb. Dobrym wyborem może okazać się biblioteka Boost.

Wykorzystanie liczb stałoprzecinkowych

Drugim sposobem na rozwiązanie naszego problemu są liczby stałoprzecinkowe. Na samym początku przyjżymy się, czym one tak na prawdę są. Na samym początku wspomnę, że nie mają one nic wspólnego z wyimaginowanym przecinkiem z pierwszego przykładu! :)

Najprościej będzie wytłumaczyć to tak: wyobraźmy sobie, że mamy do dyspozycji 8 bitów, z czego połowę z nich możemy przeznaczyć na wartość części całkowitej, a drugą połowę na wartość części ułamkowej. Na przykład:

1101.1001

Wartość takiej liczby możemy obliczyć w sposób następujący:

(unsigned) 1101.1001 = 2^3 + 2^2 + 2^0 + 2^(-1) + 2^(-4) = 13.5625

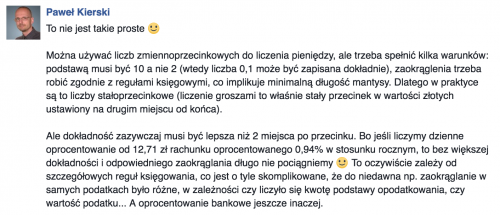
Podany przeze mnie przykład jest bardzo trywialny. W dzisiejszym czasie możemy poświęcić 64 bity pamięci na całą wartość, zostawiając przykładowo 48 bit na wartość całkowitą, a 16 bit na wartość ułamkową. Taki podział powinien nam dać maksymalną wartość całkowitą 281,474,976,710,655 (unsigned) z precyzją 0.0000152587890625. Myślę, że do liczenia prostych sum powinno nam wystarczyć. Problem może pojawić się w sytuacji, którą podał jeden z czytelników, Paweł:

Jak widać nie jest to idealne rozwiązanie, ale z racji prostoty jego implementacji warto je rozważyć, albo chociaż wiedzieć o jego istnieniu.

Arytmetyka liczb stałoprzecinkowych

Okazuje się, że operacje arytmetyczne na liczbach stałoprzecinkowych są bardzo proste i można je zrealizować w identyczny sposób, co liczby całkowite. Należy pamiętać jednak o kilku drobiazdach, o których wspomnę poniżej.

Dodawanie/Odejmowanie

Dodawanie oraz odejmowanie to operacje, które odbywają się w dokładnie taki sam sposób, jak uczono nas w podstawówce! :) Jedyna różnica jest taka, że tutaj operujemy na bitach. Zatem jak dodajemy do siebie dwa zaświecone bity, to w miejsce sumy zapisujemy 0, a 1 zostaje “w pamięci”. Tak uzyskany wynik nie wymaga żadnej korekty.

Mnożenie

Co do mnożenia, znalazłem reprezentatywny przykład obrazujący ten proces:

      0010,0010
    x 0001,1101
     ----------
       00100010
     00100010      <--- Przesunięcie o dwa, bo poprzednio mnożyliśmy przez zero
    00100010
   00100010
 --------------
   001111011010
 czyli:
  0011,11011010   <--- Musimy obciąć precyzję
 czyli:
  0011,1101

Kilka faktów:

1. Mnożenie na zasadzie znanej nam ze szkoły podstawowej :)
2. Tam, gdzie cały wiersz mnożyliśmy przez zera - pomijamy, ale pamiętajmy - że w tym miejscu również następuje przesunięcie. Uwagę zwrócić należy na jedno “podwójne” przesunięcie w przykładzie.
3. Mnożąc przez siebie dwie liczby o całkowitej wielkości x bitów, może zostać zwrócona liczba o 2x ilości bitów, zatem wynik może wymagać zaokrąglenia (utrata precyzji).

Dzielenie

Co do dzielenia liczb stałoprzecinkowych, tutaj również wszystko wygląda podobnie jak w podstawówce. Znalazłem wpis, który wszystko ładnie wyjaśnia. Poniżej przedstawiam pełny zapis z takiego dzielenia:

    1110,1(10)     <--- Wynik
--------------
 1011001: 110
- 110
---------
  1010
-  110
---------
   1000
-   110
---------
     101
-    110
---------
     1010
-     110
---------
      1000
-      110
---------
        100
-       110
---------

Kilka faktów:

1. Zawsze odejmowany jest dzielnik
2. Jeżeli część dzielnej (przy odejmowaniu) jest mniejsza od dzielnika, to do wyniku dopisujemy 0
3. Jeżeli część dzielnej (przy odejmowaniu) jest większa od dzielnika, to do wyniku dopisujemy 1
4. Po odejmowaniu zawsze zaciągamy kolejną cyfrę (bit) z prawej. Jeżeli brakuje bitów, zaciągamy zero.
5. Na końcu, jeżeli wynik jest zbyt precyzyjny, musimy go “przyciać”.

Jak widać, algorytmy działające na liczbach stałoprzecinkowych są na prawdę proste. Można pokusić się o własną implementację, albo skorzystać z już gotowej, na przykład tej. Pamiętajmy jednak, że jest to rozwiązanie niepozbawione problemów związanych z precyzją, jednak tutaj to my decydujemy, na jaką utratę precyzji możemy sobie pozwolić.

IEEE 754 - zwiększenie podstawy wykładnika

Ktoś kiedyś znalazł lek na to całe zawirowanie wokół niedokładności typów zmiennoprzecinkowych (podpowiedź w screenie wyżej :D). Tak tak, musimy wrócić do źródła, czyli standardu IEEE 754. Okazuje się, że problem związany z niedoskonałą precyzją typów float/double ma ścisły związek z podstawą potęgi używaną w standardzie. Natomiast, kiedy zamiast 2 użyjemy 10… problem znika! :) Dlaczego w takim razie typy float/double nie korzystają z 10-tki jako podstawy wykładnika? Mogę jedynie domyślać się, że jest to kompromis związany z szybkością, z jaką procesor może przeliczać kolejne potęgi liczby 2 (fizycznie wykonywane jako przesunięcie bitowe). Na szczęście istnieje implementacja, której możemy swobodnie używać wszędzie tam, gdzie nie chcemy tracić precyzji :)

Z pomocą przychodzi… Boost!

Mam nadzieję, że wszyscy czytający ten wpis znają bibliotekę Boost. Jest to zestaw użytecznych implementacji, które z jakiegoś powodu nie zostały włączone do standardu, a które ułatwiają nam życie. Jedną ze składowych tej biblioteki jest multiprecision, który zawiera pożądaną przez nas implementację - cpp_dec_float.

Sprawdziłem wszystkie przypadki, o których pisałem poprzednio i… on na prawdę daje radę! Popatrzcie sami:

// Sprawdzamy, czy możemy osiągnąć wartość 0.1
long double a = 0.1;
std::cout << std::setprecision(100) << a << std::endl;

cpp_dec_float_100 b("0.1");
std::cout << std::setprecision(100) << b << std::endl;

Wyjście programu:

0.1000000000000000055511151231257827021181583404541015625
0.1

Po prostu bajka! :) Precyzja idealna! :) Ciekawe, jak zachowa się nasza “nieskończona” pętla?

cpp_dec_float_100 counter; // Domyślna wartość jest ustawiana na 0
do {
    std::cout << "Loop " << std::endl;
    counter += cpp_dec_float_100("0.1");
} while (counter != 1.0);

Wyjście programu:

Loop
Loop
Loop
Loop
Loop
Loop
Loop
Loop
Loop
Loop

Idealnie, dziesięć obrotów pętli. Jak widać, to na prawdę działa. Sprawdźmy w takim razie, czy z Boost-em zgubimy pieniądze podczas codziennych obliczeń?

float amountOfProduct = 254.99f;
unsigned long int quantity = 100000000;
float amountOfCheckout = amountOfProduct*quantity;

std::cout << std::setprecision(30) << amountOfCheckout << std::endl;

cpp_dec_float_50 amountOfProduct2 = cpp_dec_float_50("254.99");
cpp_dec_float_50 quantity2 = cpp_dec_float_50("100000000");
cpp_dec_float_50 amountOfCheckout2 = cpp_dec_float_50(amountOfProduct2*quantity2);

std::cout << std::setprecision(30) << amountOfCheckout2 << std::endl;

Wyjście programu:

25499000832
25499000000

Jak widać, i tutaj się nie zawiodłem. Warto w takim razie rozważyć tą opcję wszędzie tam, gdzie nie możemy pozwolić sobie na przewinienia. Tutaj macie link do kompilatora online, gdzie możecie sami sprawdzić jak to działa! :)

Uwaga na stałe wyrażenia!

Jest jeszcze jeden drobny temat, który należy poruszyć w kontekście Boost multiprecision. Podczas badania tej biblioteki na początku byłem bardzo rozczarowany, bo mój przykład nie działał:

cpp_dec_float_100 b = 0.1;
std::cout << std::setprecision(100) << b << std::endl;

Dostałem taki output:

0.1000000000000000055511151231257827021181583404541015625

No, coś tutaj grubo jest nie tak - myślę. W dokumentacji jest jasno napisane, że ta biblioteka operuje na bardzo dużej precyzji, a jednak - nie różni się to nijak od long double. Po krótkiej analizie stwierdziłem, że to ja robię błąd! Problem pojawia się już podczas przekazywania przeze mnie wartości do obiektu. Niestety, ale utrata precyzji pojawia się już w momencie używania stałych typu 0.1. Ta stała już sama z siebie nie oznacza dokładnego 0.1. Co należy w takim razie zrobić?

Tada!

Zamiast stałych liczbowych przekazujmy do obiektu ciągi znakowe. Czyli nie róbmy tak:

cpp_dec_float_100 b = 0.1;

a róbmy tak:

cpp_dec_float_100 b("0.1")

Wtedy wszystko gra.

Dobra rada na przyszłość

Niezależnie od tego, z jakiego systemu skorzystamy do przeliczania pieniędzy (bądź innych danych wrażliwych na precyzję), dobrą praktyką będzie utworzenie własnej klasy, która będzie wrapperem dla zastosowanej implementacji. Jest to bardzo pomocne w chwili, kiedy z jakiegokolwiek powodu będziemy chcieli zrezygnować z obecnej implementacji na rzecz innej. Nie będziemy musieli przeszukiwać wtedy połowy systemu w celu zlokalizowania miejsc użycia starego kodu.