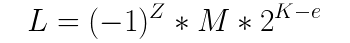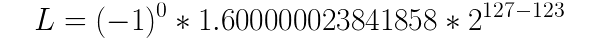Dziś krótko omówimy sobie temat liczenia pieniędzy, i dlaczego nie należy do tego celu używać typów zmiennoprzecinkowych.

Problem

Przedstawmy sobie próbkę kodu:

#include <iostream>

int main() {
    float i=0.0f;
    do {
        std::cout << "Loop " << std::endl;
        i+=0.1f;
    } while (i != 1.0f);
}

Teraz zadajmy sobie pytanie, co się wydarzy. Osoba nieświadoma problemu stwierdzi, że pętla obróci się dziesięć razy i zakończy swój bieg. Ta odpowiedź jest niestety błędna. Jest to klasyczny przykład pętli nieskończonej z użyciem liczb zmiennoprzecinkowych.

Ale dlaczego się tak stało?

Aby móc odpowiedzieć na to pytanie, należy zastanowić się nad tym, jaką dokładnie wartość dla kompilatora reprezentuje stała 0.1f. Poniżej znajduje się kod, który w idealny sposób podpowiada nam odpowiedź:

#include <iostream>
#include <iomanip>

int main() {
    std::cout << std::setprecision(10) << 0.1f << std::endl;
}

Na wyjściu programu pojawi się nam coś podobnego do:

0.1000000015

Zauważyć możemy, że 0.1f ma za sobą drobny ogon. Jest to związane ze standardem zapisu typów zmiennoprzecinkowych w pamięci naszego komputera, a konkretniej z ich ograniczoną precyzją wynikającą z zastosowania standardu IEEE-754.

Czym jest standard IEEE-754?

Standard IEEE 754 jest to standard opisujący sposób przechowaywania oraz operacji na liczbach zmiennoprzecinkowych. Definiuje on cztery typy kodowań tych liczb:

• Pojedyncza precyzja (32 bity)
• Pojedyncza rozszerzona (conajmniej 43 bity)
• Podwójna precyzja (64 bity)
• Podwójna rozszerzona (conajmniej 79 bitów)

W języku C++ obsługujemy trzy z czterech wymienionych typów kodowań:

• float - Pojedyncza precyzja
• double - Podwójna precyzja
• long double - Podwójna rozszerzona

Ponieważ mówimy o języku C++, to w dalszej części wpisu zajmiemy się wyłącznie tymi trzema rodzajami kodowań. Na początek omówimy sobie koncepty kodowania na podstawie typu pojedynczej precyzji, a później omówimy sobie różnice w stosunku do pozostałych typów kodowań.

Pojedyncza precyzja

Do dyspozycji mamy 32 bity. Rozważmy sobie przykład na podstawie naszej problematycznej wartości: 0.1.

Na obrazku powyżej można zauważyć, że pamięć przechowująca wartość zmiennej podzielona jest na trzy części:

1. Bit znaku - 1 bit
2. Zestaw bitów określający wykładnik potęgi (exponent) - 8 bitów
3. Zestaw bitów określający mantysę - 23 bity

Spójrzmy na zestaw liczb znajdujących się w drugiej linii obrazka: 0, 123 oraz 5033165. Są to binarnie reprezentacje bitu znaku, wykładnika oraz mantysy. Pierwszym krokiem, który należy uczynić w poszukiwaniu wartości liczby zmiennoprzecinkowej jest znalezienie ich znormalizowanej wartości.

Znalezienie wartości znaku

Tutaj zasada jest prosta: dla bitu niezapalonego mamy wartość dodatnią (wartość znaku równa 0), dla bitu zapalonego jest to wartość ujemna (wartość znaku równa 1).

Znalezienie wartości wykładnika

Wartość binarna dla wykładnika, to 123. Aby znaleźć właściwą wartość wykładnika, należy odjąć od jego binarnej wartości wartość stałej umownie nazwanej K. Jest to wartość stała, wynosząca:

• 127 dla liczb pojedynczej precyzji
• 1023 dla liczb podwójnej precyzji
• 16383 dla liczb podwójnej precyzji rozszerzonej

Zatem dla naszego 32-bitowego przykładu będzie to 123-127 = -4.

Znalezienie wartości mantysy

Najpierw trzeba odpowiedzieć sobie na pytanie, czym tak na prawdę jest mantysa? Z perspektywy poszukiwania jej wartości, stwierdzić możemy że mantysa to liczba, która zawsze z przodu zaczyna się od 1,. Zatem są to wartości z zakresu (2.0, 1.0>. Skoro wiemy, że mantysa zawsze będzie zaczynała się od 1, - nie ma sensu zapisywać tej wartości w pamięci. Faktycznie, mantysa zapisana w pamięci to liczby z zakresu (1.0, 0.0>.

Algorytm na znalezienie wartości mantysy jest następujący:

1. Mantysa przyjmuje wartość 0.0.
2. Wartość składnika przyjmuje wartość 1.0.
3. Przesuwamy się na pierwszy bit z lewej strony.
4. Wartość składnika dzielimy przez 2.
5. Jeżeli bit jest ustawiony (wartość 1), to do mantysy dodajemy wartość składnika.
6. Przesuwamy się o jeden bit w prawo.
7. Wróć do punktu nr 4, jeżeli nie wyszliśmy poza zakres bitów.
8. Koniec.

Tak więc, nasza mantysa będzie miała postać:

0.5 + 0.0625 + 0.03125 + 0.00390625 + 0.001953125 + 0.000244140625 + 0.0001220703125 + 0.0000152587890625 + 0.0000076293945312 + 0.0000009536743164 + 0.0000004768371582 + 0.0000001192092896

Co równa się:

0.600000023841858

Następnie dodajemy zawsze występującą jedynkę, i ostatecznie mamy:

1.600000023841858

Wyliczenie wartości liczby zmiennoprzecinkowej

Przy takim zapisie wartość konkretnej liczby zmiennoprzecinkowej osiągnąć można poprzez wykonanie obliczenia na podstawie wzoru:

Po podstawieniu wyznaczonych przez nas wartości wychodzi nam wzór:

Ostatecznie wychodzi nam wartość 0.100000001490116119384765625.

Pozostałe typy kodowania

Zasada działania na każdym typie precyzji na ogół jest taka sama¹. Zmienia się jedynie rozkład bitów przeznaczonych na wykładnik oraz mantysę, co pozwala na zwiększenie precyzji. Zatem:

• Podwójna precyzja: 1 bit znaku, 52 bity dla mantysy, 11 bitów na wykładnik
• Podwójna rozszerzona: 1 bit znaku, 64 bity dla mntysy, pozostała ilość bitów dla wykładnika

Dla każdego typu kodowania zmienia się również liczba K (znana również jako obciążenie wykładnika), ale o tym pisałem już wcześniej.

Wartości specjalne

Standard opisuje również kilka wartości specjalnych, które nie są wyrażane liczbowo. Należą do nich:

• NaN - Not a Number. Wszystkie bity mantysy oraz wykładnika są zapalone. Bit wykładnika znaku nie jest zapalony.
• Inf - Positive infinity. Bit znaku niezapalony, wszystkie bity wykładnika są zapalone. Bity mantysy nie są zapalone.
• -Inf - Negative infinity. Bit znaku zapalony, wszystkie bity wykładnika są zapalone. Bity mantysy nie są zapalone.

Zgubiona precyzja

Używając omawianego tutaj formatu zapisu liczb zmiennoprzecinkowych, nie jesteśmy w stanie zapisać każdej liczby z zakresu. Z tego powodu często mówi się o tym formacie jako o liczbach pseudo-zmiennoprzecinkowych. Używając tego typu należy zawsze mieć na uwadze precyzję, przez którą nigdy nie będziemy mieli pewności co do dokładnej wartości przechowywanej wewnątrz zmiennej. Ważną jest również informacja, że to do kompilatora należy decyzja o tym, czy liczba spoza zakresu obsługiwanych wartości zostanie zaokrąglona w górę lub w dół.

Uwaga.
Więcej na temat liczb zmiennoprzecinkowych i standardu IEEE 754 możecie przeczytać w książce Zrozumieć Programowanie autorstwa Gynvael’a Coldwind’a.

Wróćmy do liczenia pieniędzy…

Jeżeli kwoty pieniężne liczymy używając liczb zmiennoprzecinkowych, to na bank gdzieś nam się te pieniądze będą gubić. Na pytanie dlaczego odpowiedzieliśmy sobie omawiając budowę formatu liczb zmiennoprzecinkowych, ale dla utrwalenia przeanalizujmy sobie poniższy program:

#include <iostream>
#include <iomanip>

int main() {
    float amountOfProduct = 254.99f;
    unsigned long int quantity = 100000000;
    float amountOfCheckout = amountOfProduct*quantity;

    std::cout << std::setprecision(15) << amountOfCheckout << std::endl;
}

Wyjście programu jest następujące:

25499000832

Ktoś przez błąd systemu będzie osiem stówek w plecy! I nagle odezwą się ci, którzy zapytają: “Kto mnoży przez tak wielką liczbę?”. Niestety, takie rzeczy bardzo często liczy się w różnego rodzaju raportach sprzedażowych. Jeżeli prowadzi się biznes na światową skalę, to bardzo łatwo jest dotrzeć do takich liczb.

Rozwiązaniem na ten problem jest użycie typu całkowitego, gdzie jako jednostkę potraktujemy grosza. Mamy zatem taki kod:

#include <iostream>
#include <iomanip>

int main() {
    unsigned long int amountOfProduct = 25499;
    unsigned long int quantity = 100000000;
    unsigned long int amountOfCheckout = amountOfProduct*quantity;

    std::cout << std::setprecision(15) << amountOfCheckout << std::endl;
}

którego wyjście jest następujące:

2549900000000

Wszystko liczy się tak, jak liczyć się powinno. Dopiero po wykonaniu wszystkich kalkulacji możemy podzielić wynik przez sto i przedstawić liczbę w formie przyjaznej klientowi.

Konkluzja

Zakończyć swój wywód mogę tylko jednym stwierdzeniem: używajmy typów zmiennoprzecinkowych wszędzie tam, gdzie możemy pozwolić sobie na drobne przewinienia. Na pewno nie używajmy ich do liczenia pieniędzy.

¹ Istnieje kilka drobnych różnic, o których nie wspominam ze względu na skomplikowanie poziomu merytoryki materiału.

Kalkulator, którego używałem: https://www.h-schmidt.net/FloatConverter/IEEE754.html